Distributed Computing for Distributed Control

Diffusive Realization

A theoretical framework of diffusive realization has been introduced for state-realizations of linear operators that are solution to certain linear operator-differential equations in bounded domains. The theory has been applied to a Lyapunov equation arising from distributed optimal control. Numerical methods have been established and a first implementation on a FPGA has been achieved. This method is a good candidate for distributed computing implementation of real-time distributed optimal control in large system arrays.

Semi-decentralized Approximations of Riccatti Equations for Distributed Control

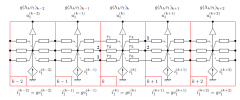
A method has been introduced to realize semi-decentralized optimal control of large linear distributed systems for real-time applications. It applies to systems modeled by linear partial differential equations with observation and control distributed over the whole domain. This is a strong assumption, but it does not mean that actuators and sensors are actually continuously distributed. Models satisfying such assumption may be derived from homogenization of systems with periodic distribution of actuators and sensors. The method is based on a functional calculus for self-adjoint operators. It has been shown to be well suited for being implemented with distributed periodic analog circuits.