Abstract:
The aim of the Claytronics project is to build spherical micro-robots, called catoms for Claytronics atoms able to stick to each other and able to move around each other. An ensemble of catoms is therefore a huge modular self-reconfigurable robot. However, the shape of these catoms have not been studied yet and remains a difficult problem as there are numerous constraints to respect.
In this article, we propose a quasi-spherical catom which answers to all the constraints to build programmable matter.
Our work at a glance
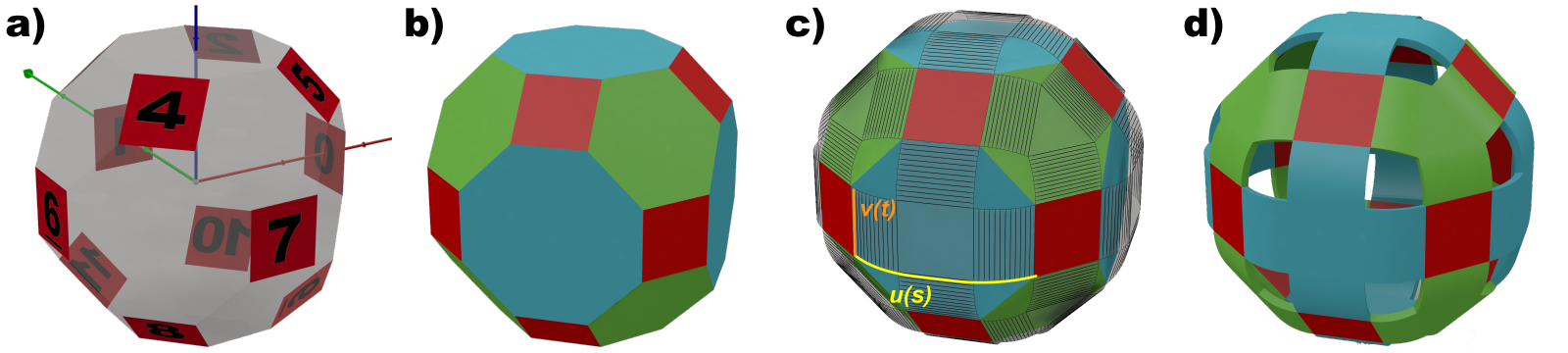
At contacts points of cells in Face-Centered Cubic Lattice, we place 12 squares (Fig. 1.1). We connect these squares by 8 hexagons and 6 octagons in order to obtain a regular polyedron (named truncated cuboctahedron). But this shape is not well adapted for rotating. Then we replace hexagons and octagons planes by curves in order to obtain continuous surfaces as shown in the Figure 1.3.
Dimensions of catoms depending on the radius r:
Connectors: square of size c
`c=(2r)/(3+sqrt(2))~~0.45r`
Actuators:
`l_1~~2xx0.287xxr`
`l_2~~2xx0.356xxr`
Paper and conference slides:
Bibtex
@inproceedings{dpb13:ip,
domainehal = {INFO:INFO_MC, INFO:INFO_NI, INFO:INFO_MO},
equipe = {omni},
author = {Piranda, Benoit and Bourgeois, Julien},
title = {Design of quasi-spherical modules for building programmable matter},
booktitle = {DARS 2016, 13th IEEE International Symposium on Distributed Autonomous Robotic Systems},
pages = {--},
address = {Londo, UK},
month = {oct},
year = {2016},
}
Videos
The first video presents three interesting points of our work:
- First, a 3D catom can be construct from a planar unfold.
- 3D catoms are placed in a regular Face-Centered Cubic lattice.
- Rotations allows 3D catoms to move from a position of the grid to an other one.
The second video shows different possible motions of a catom around another one.